Beschrijving
Welke relatie hebben de getallen 2, 3, 4, 8, 10, 12, 20, 48 en 240 met elkaar? Ze horen allemaal tot het netwerk van getalrelaties rond het getal 24.
Zomaar een voorbeeld van het belang van getallen voor het rekenonderwijs. Niet voor niets vormt de leerlijn getallen en getalrelaties de basis voor optellen en aftrekken, vermenigvuldigen en delen.
In je groep wil je rekening houden met het persoonlijke niveau van de leerlingen. En na een toets komen die verschillen extra naar boven drijven. De meeste leerlingen gaan goed mee, maar een enkele leerling vertoont uitval. De Kerndoeltrainer helpt je verder om de juiste oefening te vinden voor het specifieke probleem waarmee je leerling zit.
Elk deel behandelt namelijk een bepaald niveau van de leerlijn getallen en getalrelaties en op basis van je analyses kun je gerichte oefeningen aanbieden die je leerling op dat moment nodig heeft. En heeft je leerling op verschillende onderdelen uitval? Geen probleem, want het maakt niet uit op welk niveau je leerling begint. Er kan van leerprobleem naar leerprobleem gesprongen worden, want alle leerdoelen van de gehele leerlijn staan in elk deel overzichtelijk opgesomd.
De Kerndoeltrainer Getallen & Getalrelaties omvat alleen oefeningen rond de getallen en sluit goed aan bij kerndoel 26. We hebben dit kerndoel in concrete leerdoelen per niveau uitgewerkt, die elk een deelgebied van de leerlijn behandelt.
Kerndoeltrainer Getallen & Getalrelaties E bevat gevarieerde en betekenisvolle oefeningen rond de getallen t/m 100.000 met de volgende leerdoelen:
Getalbetekenis t/m 100.000
In het blok Getalbetekenis wordt een relatie gelegd tussen cijfers en getallen door ze te benoemen en wordt de betekenis van verschillende getallen bekeken; het grote getal (herkenbaar door scheidingspunt), het kommagetal (herkenbaar door komma), het breukgetal (herkenbaar door teller en noemer) en het Romeinse cijfer (XII).
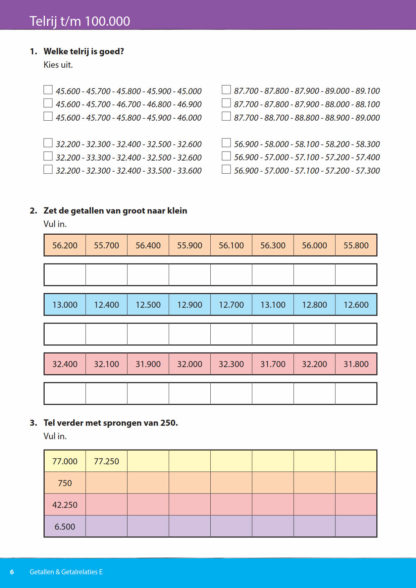
Telrij t/m 100.000
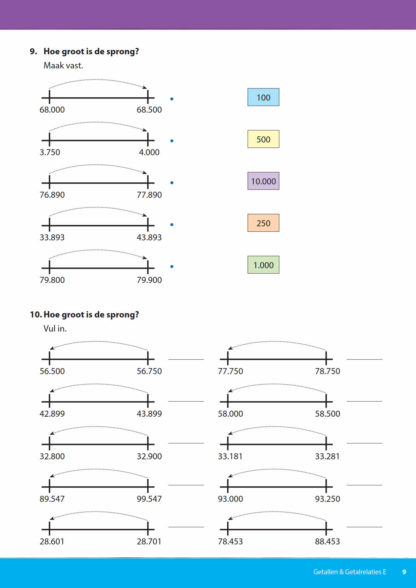
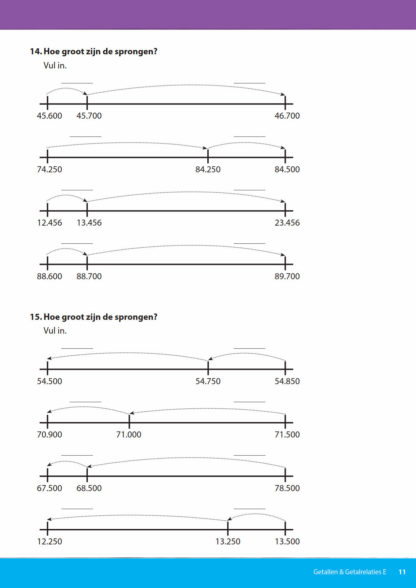
In het blok Telrij wordt geoefend met verder- of terugtellen in sprongen van 100, 250, 500, 1.000 of 10.000. Ook wordt gekeken hoe groot een sprong is tijdens het verder- of terugtellen; met regelmatige of onregelmatige sprongen.
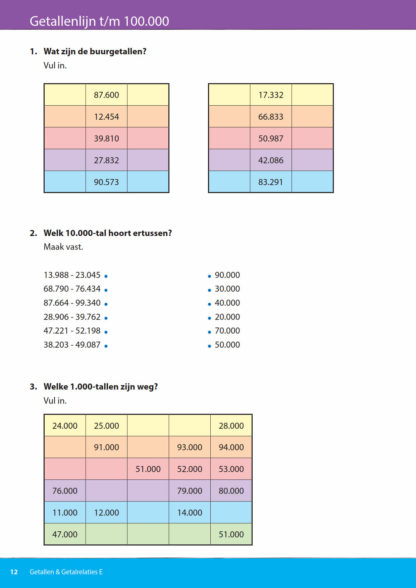
Getallenlijn t/m 100.000
In het blok Getallenlijn gaat het om de relatieve positie van getallen ten opzichte van andere getallen en wordt de absolute positie van het getal aan de getallenlijn bekeken, waarbij de exact positie niet meer relevant is. Bijzondere aandacht is er voor met een cijfer achter de komma en breukgetallen t/m 100.
Getallen op volgorde t/m 100.000
In het blok Getallen op volgorde gaat het zowel om getallen in de telrij, als om hoeveelheidsgetallen. Begrippen als klein, groot, minder, meer of evenveel komen hier aan de orde en is er aandacht voor kommagetallen en breukgetallen t/m 100.
Getalrelaties t/m 100.000
In het blok Getalrelaties wordt bekeken hoe getallen in relatie tot elkaar staan. Hierbij gaat het om kommagetallen en breukgetallen (8,25 & 8).
Ronde getallen t/m 100.000
In het blok Ronde getallen worden de duizendtallen en tienduizendtallen opgezocht. Door naar deze ronde getallen verder of terug te springen wordt het rekenen makkelijker gemaakt.
Getalstructuur t/m 100.000
In het blok Getalstructuur worden op een gestructureerde manier met eenheden, tientallen, honderdtallen, duizendtallen en tienduizendtallen, getallen samengesteld of opgedeeld. Hierbij wordt het positieschema (TD, D, H, T, E) gebruikt. Ook wordt de waarde van het cijfer in een getal bekeken.